Static friction (or stiction) arises due to surface characteristics at the microscopic level (e.g., mechanical interference of surface imperfections, electrostatic, and/or Van der Waals forces).

Two objects in static contact need to have a force fₚ applied parallel to the surface of contact sufficient to break stiction. Once the objects are moving, kinetic (dynamic) friction takes over. It is possible to accelerate one body sliding across another body with a force that would have been too small to break stiction. In essence, stiction will create a contrary force canceling out any force too small to break stiction (see Figure 2).

Figure 2: Idealized Stiction/Sliding Friction Model

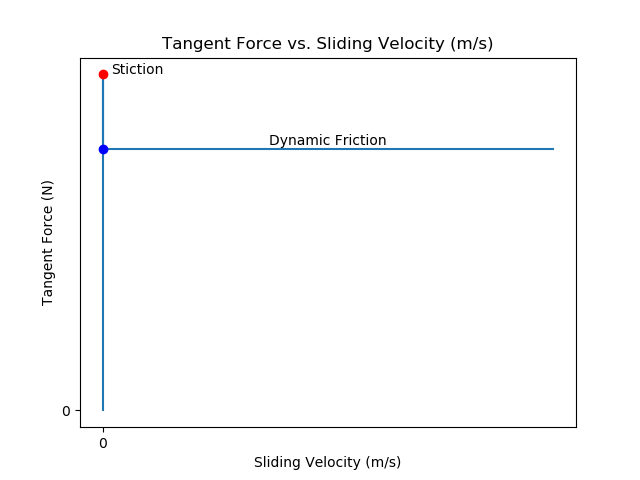
In idealized stiction, tangent force fₜ is equal and opposite to the pushing force fₚ up to the point where that force is sufficient to break stiction (the red dot in Figure 2). At that point, the tangent force immediately becomes a constant force based on the kinetic coefficient of friction. There are obvious discontinuities in this function which do not occur in reality, but this can be a useful approximation and can be implemented in this form using constraints that can be enabled and disabled discontinuously. However, here we are looking for a continuous model that can produce reasonable behavior using only unconstrained differential equations. With this model we can also capture the empirically-observed Stribeck effect where the friction force declines with increasing slip velocity until it reaches the kinetic friction level.

Figure 3: Stribeck function for stiction

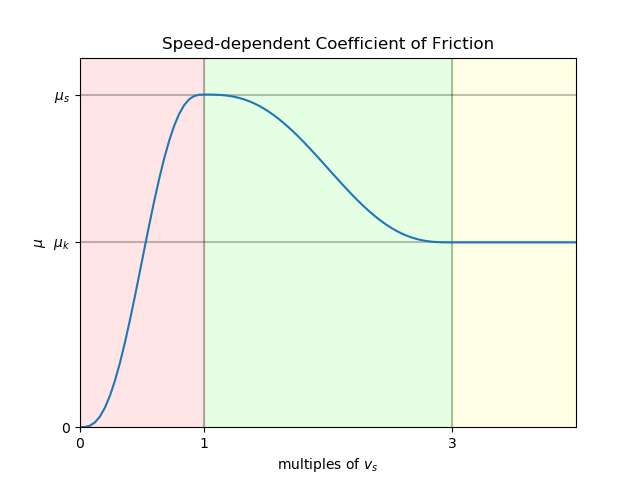
The Stribeck model is a variation of Coulomb friction, where the frictional (aka tangential) force is proportional to the normal force as:

fₜ = μ⋅fₙ,

In the Stribeck model, the coefficient of friction, μ, is replaced with a slip speed-dependent function:

fₜ = μ(s)⋅fₙ,

where s is a unitless multiple of a new parameter: slip tolerance (vₛ). Rather than modeling perfect stiction, it makes use of an allowable amount of relative motion to approximate stiction. When we refer to "relative motion", we refer specifically to the relative translational speed of two points Ac and Bc defined to instantly be located at contact point Co and moving with bodies A and B, respectively.

The function, as illustrated in Figure 3, is a function of the unitless multiple of vₛ. The domain is divided into three intervals:

s ∈ [0, 1): the coefficient of friction rises smoothly from zero to the static coefficient of friction, μs.
s ∈ [1, 3): The coefficient of friction falls smoothly from μs to the kinetic (dynamic) coefficient of friction, μd.
s ∈ [3, ∞): Coefficient of friction is held constant at μd.

Other than the residual "creep" velocity limited by vₛ, which can be arbitrarily small (in theory; see set_stiction_tolerance() for practical considerations), this model produces a reasonably good approximation of Coulomb friction. Its primary drawback is that the model is numerically very stiff in the stiction region, which requires either small step sizes with an explicit integrator, or use of a more-stable implicit integrator.

Note: When modeling the multibody system as discrete (refer to the Choice of Time Advancement Strategy section), the model assumes both static and kinetic coefficients of friction to be equal and the static coefficient of friction is ignored.