LinearBushingRollPitchYaw< T > Class Template Reference

Detailed Description

template<typename T>
class drake::multibody::LinearBushingRollPitchYaw< T >

This ForceElement models a massless flexible bushing that connects a frame A of a link (body) L0 to a frame C of a link (body) L1.

The bushing can apply a torque and force due to stiffness (spring) and dissipation (damper) properties. Frame B is the bushing frame whose origin Bo is halfway between Ao (A's origin) and Co (C's origin) and whose unit vectors 𝐁𝐱, 𝐁𝐲, 𝐁𝐳 are "halfway" (in an angle-axis sense) between the unit vectors of frame A and frame C. Frame B is a "floating" frame in the sense that it is calculated from the position and orientation of frames A and C (B is not welded to the bushing).

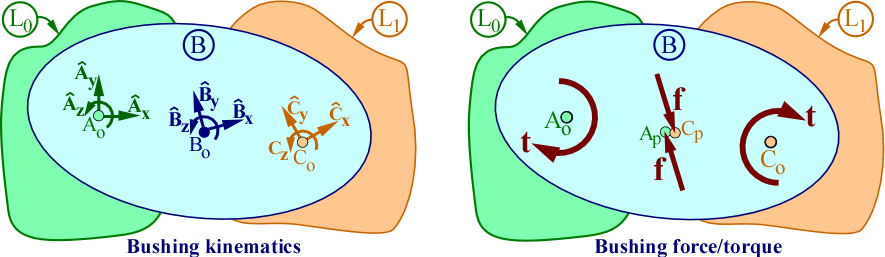
The set of forces on frame C from the bushing is equivalent to a torque 𝐭 on frame C and a force 𝐟 applied to a point Cp of C. The set of forces on frame A from the bushing is equivalent to a torque −𝐭 on frame A and a force −𝐟 applied to a point Ap of A. Points Ap and Cp are coincident with Bo (frame B's origin).

This "quasi-symmetric" bushing force/torque model was developed at Toyota Research Institute and has advantages compared to traditional bushing models because it employs a bushing-centered "symmetric" frame B and it ensures the moment of −𝐟 on A about Ao is equal to the moment of 𝐟 on C about Co. Traditional models differ as they lack a "symmetric" frame B and apply −𝐟 at Ao, which means the moment of −𝐟 on A about Ao is always zero. Note: This bushing model is not fully symmetric since the orientation between frames A and C is parameterized with roll-pitch-yaw angles [q₀ q₁ q₂]. Since these angles have an inherent sequence, they are not mathematically symmetric.

The torque model depends on spring-damper "gimbal" torques τ ≜ [τ₀ τ₁ τ₂] which themselves depend on roll-pitch-yaw angles q ≜ [q₀ q₁ q₂] and rates q̇ = [q̇₀ q̇₁ q̇₂] via a diagonal torque-stiffness matrix K₀₁₂ and a diagonal torque-damping matrix D₀₁₂ as

    ⌈ τ₀ ⌉     ⌈k₀    0    0⌉ ⌈ q₀ ⌉     ⌈d₀    0    0⌉ ⌈ q̇₀ ⌉
τ ≜ | τ₁ | = − | 0   k₁    0| | q₁ |  −  | 0   d₁    0| | q̇₁ |
    ⌊ τ₂ ⌋     ⌊ 0    0   k₂⌋ ⌊ q₂ ⌋     ⌊ 0    0   d₂⌋ ⌊ q̇₂ ⌋ 

where k₀, k₁, k₂ and d₀, d₁, d₂ are torque stiffness and damping constants and must have non-negative values.

Note

τ does not represent a vector expressed in one frame. Instead it is regarded as a 3x1 array of torque scalars associated with roll-pitch yaw.

As discussed in the Advanced section below, τ is not 𝐭 (τ ≠ 𝐭).

This is a "linear" bushing model as gimbal torque τ varies linearly with q and q̇ as τ = τᴋ + τᴅ where τᴋ = −K₀₁₂ ⋅ q and τᴅ = −D₀₁₂ ⋅ q̇.

The bushing model for the net force 𝐟 on frame C from the bushing depends on scalars x, y, z which are defined so 𝐫 (the position vector from Ao to Co) can be expressed in frame B as 𝐫 ≜ p_AoCo = [x y z]ʙ = x 𝐁𝐱 + y 𝐁𝐲 + z 𝐁𝐳. The model for 𝐟 uses a diagonal force-stiffness matrix Kxyᴢ, a diagonal force-damping matrix Dxyᴢ, and defines fx, fy, fz so 𝐟 = [fx fy fz]ʙ.

⌈ fx ⌉      ⌈kx    0    0⌉ ⌈ x ⌉     ⌈dx    0    0⌉ ⌈ ẋ ⌉
| fy | =  − | 0   ky    0| | y |  −  | 0   dy    0| | ẏ |
⌊ fz ⌋      ⌊ 0    0   kz⌋ ⌊ z ⌋     ⌊ 0    0   dz⌋ ⌊ ż ⌋ 

where kx, ky, kz and dx, dy, dz are force stiffness and damping constants and must have non-negative values.

Note

This is a "linear" bushing model as the force 𝐟 varies linearly with 𝐫 and 𝐫̇̇ as 𝐟 = 𝐟ᴋ + 𝐟ᴅ where 𝐟ᴋ = −Kxyz ⋅ 𝐫 and 𝐟ᴅ = −Dxyz ⋅ 𝐫̇̇.

This bushing's constructor sets the torque stiffness/damping constants [k₀ k₁ k₂] and [d₀ d₁ d₂] and the force stiffness/damping constants [kx ky kz] and [dx dy dz]. The examples below demonstrate how to model various joints that have a flexible (e.g., rubber) mount. The damping values below with ? may be set to 0 or a reasonable positive number.

Bushing type	torque constants	force constants
z-axis revolute joint	k₀₁₂ = [k₀ k₁ 0]	kxyz = [kx ky kz]
	d₀₁₂ = [d₀ d₁ ?]	dxyz = [dx dy dz]
x-axis prismatic joint	k₀₁₂ = [k₀ k₁ k₂]	kxyz = [0 ky kz]
	d₀₁₂ = [d₀ d₁ d₂]	dxyz = [? dy dz]
Ball and socket joint	k₀₁₂ = [0 0 0]	kxyz = [kx ky kz]
	d₀₁₂ = [? ? ?]	dxyz = [dx dy dz]
Weld/fixed joint	k₀₁₂ = [k₀ k₁ k₂]	kxyz = [kx ky kz]
	d₀₁₂ = [d₀ d₁ d₂]	dxyz = [dx dy dz]

Angles q₀, q₁, q₂ are calculated from frame C's orientation relative to frame A, with [−π < q₀ ≤ π, −π/2 ≤ q₁ ≤ π/2, −π < q₂ ≤ π], hence, there is no angle wrapping and torque stiffness has a limited range. Gimbal torques τ can be discontinuous if one of q₀, q₁, q₂ is discontinuous and its associated torque spring constant is nonzero. For example, τ₂ is discontinuous if k₂ ≠ 0 and the bushing has a large rotation so q₂ jumps from ≈ −π to π. τ can also be discontinuous if one of q̇₀, q̇₁, q̇₂ is discontinuous and its associated torque damper constant is nonzero. For example, τ₀ is discontinuous if d₀ ≠ 0 and q̇₀ is undefined (which occurs when pitch = q₁ = π/2). Note: Due to the relationship of 𝐭 to τ shown below, 𝐭 is discontinuous if τ is discontinuous.

As shown below, there are multiple ways to estimate torque and force stiffness and damping constants. Use a method or combination of methods appropriate for your application. For example, some methods are more useful for a real physical bushing whereas other methods (called "penalty methods") can be more useful when replacing an ideal joint (such as a revolute or fixed/weld joint) with a bushing.

Consider a penalty method if you want a bushing to substitute for a "hard" constraint (e.g., an ideal joint). Since a bushing is inherently compliant it will violate a hard constraint somewhat. The stiffer the bushing, the more accurately it enforces the hard constraint, but at a cost of more computational time. To balance accuracy versus time, consider your tolerance for constraint errors. For example, is it OK for your bushing to displace xₘₐₓ = 1 mm for an estimated Fxₘₐₓ = 100 N? Also, one way to choose a force damping constant dx is by choosing a "reasonably small" settling time tₛ, where settling time tₛ is the interval of time for a system to settle to within 1% (0.01) of an equilibrium solution). Is tₛ = 0.01 s negligible for a robot arm with a 10 s reach maneuver?

How to choose a torque stiffness constant k₀ or damping constant d₀.

The estimate of stiffness k₀ depends on whether you are modeling a physical bushing (consider stiffness methods 1 or 2 below) or whether you are using a bushing to replace an ideal joint such as a revolute or fixed/weld joint (consider stiffness "penalty methods" 3 or 4 below).

1. Use a static experiment, e.g., apply a known moment load Mx, measure the associated angular displacement Δq (radians), and estimate k₀ = Mx / Δq.
2. Use FEA (finite element analysis) software to estimate k₀.
3. Pick a desired maximum angular displacement qₘₐₓ, estimate a maximum moment load Mxₘₐₓ, and estimate k₀ = Mxₘₐₓ / qₘₐₓ (units of N*m/rad).
4. Choose a characteristic moment of inertia I₀ (directionally dependent), choose a desired angular frequency ωₙ > 0 (in rad/s) and estimate k₀ = I₀ ωₙ² (units of N*m/rad).

The estimate of damping d₀ depends on whether you are modeling a physical bushing (consider damping method 1 below) or whether you are using a bushing to enforce a constraint (consider damping methods 2 or 3 below).

1. Use experiments to estimate a damping ratio ζ and settling time tₛ. Compute "undamped natural frequency" ωₙ from ζ and tₛ (as shown below in the Advanced section), then d₀ = 2 ζ k₀ / ωₙ (units of N*m*s/rad).
2. Choose a damping ratio ζ (e.g., ζ = 1, critical damping) and a desired settling time tₛ, calculate ωₙ (as shown below in the Advanced section), then d₀ = 2 ζ k₀ / ωₙ (units of N*m*s/rad).
3. Choose a damping ratio ζ (e.g., ζ = 1, critical damping), estimate a characteristic moment of inertia and calculate d₀ = 2 ζ √(I₀ k₀).

Refer to Advanced bushing stiffness and damping for more details.

How to choose a force stiffness constant kx or damping constant dx.

The estimate of stiffness kx depends on whether you are modeling a real bushing (consider stiffness methods 1 or 2 below) or whether you are using a bushing to replace an ideal joint such as a revolute or fixed/weld joint (consider stiffness "penalty methods" 3 or 4 below).

1. Use a static experiment, e.g., apply a known force load Fx, measure the associated displacement (stretch) Δx (in meters), and estimate kx = Fx / Δx.
2. Use FEA (finite element analysis) software to estimate kx (units of N/m).
3. Pick a desired maximum displacement xₘₐₓ, estimate a maximum force load Fxₘₐₓ, and estimate kx = Fxₘₐₓ / xₘₐₓ (units of N/m).
4. Choose a characteristic mass m (which may be directionally dependent), choose a desired angular frequency ωₙ > 0 (in rad/s) and estimate kx = m ωₙ² (units of N/m).

The estimate of damping dx depends on whether you are modeling a physical bushing (consider damping method 1 below) or whether you are using a bushing to enforce a constraint (consider damping methods 2 or 3 below).

1. Use experiments to estimate a damping ratio ζ and settling time tₛ. Compute "undamped natural frequency" ωₙ from ζ and tₛ (as shown below in the Advanced section), then dx = 2 ζ kx / ωₙ (units of N*s/m).
2. Choose a damping ratio ζ (e.g., ζ = 1, critical damping) and a desired settling time tₛ, calculate ωₙ (as shown below in the Advanced section), then dx = 2 ζ kx / ωₙ (units of N*s/m).
3. Choose a damping ratio ζ (e.g., ζ = 1, critical damping), estimate a characteristic mass m and calculate dx = 2 ζ √(m kx) (units of N*s/m).

Refer to Advanced bushing stiffness and damping for more details.

Advanced: Relationship of 𝐭 to τ.

To understand how "gimbal torques" τ relate to 𝐭, it helps to remember that the RollPitchYaw class documentation states that a Space-fixed (extrinsic) X-Y-Z rotation with roll-pitch-yaw angles [q₀ q₁ q₂] is equivalent to a Body-fixed (intrinsic) Z-Y-X rotation by yaw-pitch-roll angles [q₂ q₁ q₀]. In the context of "gimbal torques", the Body-fixed Z-Y-X rotation sequence with angles [q₂ q₁ q₀] is physical meaningful as it produces torques associated with successive frames in a gimbal as τ₂ 𝐀𝐳, τ₁ 𝐏𝐲, τ₀ 𝐂𝐱, where each of 𝐀𝐳, 𝐏𝐲, 𝐂𝐱 are unit vectors associated with a frame in the yaw-pitch-roll rotation sequence and 𝐏𝐲 is a unit vector of the "pitch" intermediate frame. As described earlier, torque 𝐭 is the moment of the bushing forces on frame C about Cp. Scalars tx, ty, tz are defined so 𝐭 can be expressed 𝐭 = [tx ty tz]ᴀ = tx 𝐀𝐱 + ty 𝐀𝐲 + tz 𝐀𝐳. As shown in code documentation, the relationship of [tx ty tz] to [τ₀ τ₁ τ₂] was found by equating 𝐭's power to τ's power as 𝐭 ⋅ w_AC = τ ⋅ q̇.

⌈ tx ⌉      ⌈ τ₀ ⌉            ⌈ cos(q₂)/cos(q₁)  sin(q₂)/cos(q₁)   0 ⌉
| ty | = Nᵀ | τ₁ |  where N = |   −sin(q2)            cos(q2)      0 |
⌊ tz ⌋      ⌊ τ₂ ⌋            ⌊ cos(q₂)*tan(q₁)   sin(q₂)*tan(q₁)  1 ⌋

Advanced: More on how to choose bushing stiffness and damping constants.

The basics on how to choose bushing stiffness and damping constants are at:

• How to choose torque stiffness and damping constants
• How to choose force stiffness and damping constants

The list below provides more detail on: The performance tradeoff between high stiffness and long simulation time; loads that affect estimates of Mxₘₐₓ or Fxₘₐₓ; and how a linear 2ⁿᵈ-order ODE provides insight on how to experimentally determine stiffness and damping constants.

• Stiffness [k₀ k₁ k₂] and [kx ky kz] affect simulation time and accuracy. Generally, a stiffer bushing better resembles an ideal joint (e.g., a revolute joint or fixed/weld joint). However (depending on integrator), a stiffer bushing usually increases numerical integration time.
• An estimate for a maximum load Mxₘₐₓ or Fxₘₐₓ accounts for gravity forces, applied forces, inertia forces (centripetal, Coriolis, gyroscopic), etc.
• One way to determine physical stiffness and damping constants is through the mathematical intermediaries ωₙ (units of rad/s) and ζ (no units). The constant ωₙ (called "undamped natural frequency" or "angular frequency") and constant ζ (called "damping ratio") relate to the physical constants mass m, damping constant dx, and stiffness constant kx via the following prototypical linear constant-coefficient 2ⁿᵈ-order ODEs.

   m ẍ +     dx ẋ +  kx x = 0   or alternatively as
     ẍ + 2 ζ ωₙ ẋ + ωₙ² x = 0   where ωₙ² = kx/m,  ζ = dx / (2 √(m kx))

  ωₙ and ζ also appear in the related ODEs for rotational systems, namely

   I₀ q̈ +     d₀ q̇ +  k₀ q = 0   or alternatively as
      q̈ + 2 ζ ωₙ q̇ + ωₙ² q = 0   where ωₙ² = k₀/I₀,  ζ = d₀ / (2 √(I₀ k₀))
  

  One way to determine ωₙ is from settling time tₛ which approximates the time for a system to settle to within a specified settling ratio of an equilibrium solutions. Typical values for settling ratio are 1% (0.01), 2% (0.02), 5% (0.05), and 10% (0.10).
  • When ζ < 0.7 (underdamped), a commonly used approximation is ωₙ ≈ -ln(settling_ratio) / (ζ tₛ) which for settling ratios 0.01 and 0.05 give ωₙ ≈ 4.6 / (ζ tₛ) and ωₙ ≈ 3 / (ζ tₛ). Another commonly used approximation is ωₙ ≈ -ln(settling_ratio √(1- ζ²)) / (ζ tₛ). See https://en.wikipedia.org/wiki/Settling_time or the book Modern Control Engineering by Katsuhiko Ogata. Although these approximate formulas for ωₙ are common, they are somewhat inaccurate. Settling time for underdamped systems is discontinuous and requires solving a nonlinear algebraic equation (an iterative process). For more information, see http://www.scielo.org.co/pdf/rfiua/n66/n66a09.pdf [Ramos-Paja, et. al 2012], "Accurate calculation of settling time in second order systems: a photovoltaic application". Another reference is https://courses.grainger.illinois.edu/ece486/sp2020/laboratory/docs/lab2/estimates.html
  • When ζ ≈ 1 (critically damped), ωₙ is determined by choosing a settling ratio and then solving for (ωₙ tₛ) via the nonlinear algebraic equation (1 + ωₙ tₛ)*exp(-ωₙ tₛ) = settling_ratio.

    Settling ratio	ωₙ
    0.01	6.64 / tₛ
    0.02	5.83 / tₛ
    0.05	4.74 / tₛ
    0.10	3.89 / tₛ

    See https://electronics.stackexchange.com/questions/296567/over-and-critically-damped-systems-settling-time
  • When ζ ≥ 1.01 (overdamped), ωₙ ≈ -ln(2 settling_ratio sz/s₂) / (s₁ tₛ) where sz = √(ζ² - 1), s₁ = ζ - sz, s₂ = ζ + sz. The derivation and approximation error estimates for this overdamped settling time formula is below.
• For a real physical bushing, an experiment is one way to estimate damping constants. For example, to estimate a torque damping constant d₀ associated with underdamped vibrations (damping ratio 0 < ζ < 1), attach the bushing to a massive rod, initially displace the rod by angle Δq, release the rod and measure q(t). From the q(t) measurement, estimate decay ratio (the ratio of successive peak heights above the final steady-state value) calculate logarithmic decrement δ = -ln(decay_ratio), calculate damping ratio ζ = √(δ² / (4π² + δ²)), then calculate d₀ using d₀ = 2 ζ √(I₀ k₀) or d₀ = 2 ζ k₀ / ωₙ. For more information, see https://en.wikipedia.org/wiki/Damping_ratio#Logarithmic_decrement

Derivation: Approximate formula for overdamped settling time.

Since a literature reference for this formula was not found, the derivation below was done at TRI (it has not been peer reviewed). This formula results from the "dominant pole" solution in the prototypical constant-coefficient linear 2ⁿᵈ-order ODE. For ẋ(0) = 0, mathematics shows poles p₁ = -ωₙ s₁, p₂ = -ωₙ s₂, where sz = √(ζ² - 1), s₁ = ζ - sz, s₂ = ζ + sz. and

 x(t) / x(0) = p₂/(p₂-p₁) exp(p₁ t) - p₁/(p₂-p₁) exp(p₂ t)
             = s₂/(s₂-s₁) exp(p₁ t) - s₁/(s₂-s₁) exp(p₂ t)
             =  k/( k-1 ) exp(p₁ t) -  1/( k-1 ) exp(p₂ t) where k = s₂ / s₁
             ≈  k/( k-1 ) exp(p₁ t)                        since p₁ > p₂

Note: k = s₂ / s₁ is real, k > 0, s₂ = k s₁, and p₁ > p₂ (p₁ is less negative then p₂), so exp(p₁ t) decays to zero slower than exp(p₂ t) and exp(p₁ t) ≫ exp(p₂ t) for sufficiently large t. Hence we assume exp(p₂ t) ≈ 0 (which is why p₁ is called the "dominant pole"). Next,

  k/(k - 1) = s₂ / s₁ / (s₂/s₁ -1) = s₂ / (s₂ - s₁) = s₂ / (2 sz),  so
  x(t) / x(0)  ≈  s₂ / (2 sz) exp(-s₁ ωₙ t),                        hence
  settling_ratio ≈ s₂ / (2 sz) exp(-s₁ ωₙ tₛ),                      finally
  ωₙ ≈ -ln(settling_ratio 2 sz / s₂) / (s₁ tₛ)

The table below shows that there is little error in this approximate formula for various settling ratios and ζ, particularly for ζ ≥ 1.1. For 1.0 ≤ ζ < 1.1, the critical damping estimates of ωₙ work well.

Settling ratio	ζ = 1.01	ζ = 1.1	ζ = 1.2	ζ = 1.3	ζ = 1.5
0.01	1.98%	0.005%	2.9E-5%	1.6E-7%	2.4E-12%
0.02	2.91%	0.016%	1.8E-4%	2.1E-6%	1.6E-10%
0.05	5.10%	0.076%	2.3E-3%	7.0E-5%	4.4E-8%
0.10	8.28%	0.258%	1.6E-2%	1.0E-3%	3.3E-6%

Note: There is a related derivation in the reference below, however, it needlessly makes the oversimplified approximation k/(k - 1) ≈ 1. https://electronics.stackexchange.com/questions/296567/over-and-critically-damped-systems-settling-time

Note

The complete theory for this bushing is documented in the source code. Please look there if you want more information.

Template Parameters

T	The underlying scalar type. Must be a valid Eigen scalar.

See also

math::RollPitchYaw for definitions of roll, pitch, yaw [q₀ q₁ q₂].

Note

Per issue #12982, do not directly or indirectly call the following methods as they have not yet been implemented and throw an exception: CalcPotentialEnergy(), CalcConservativePower(), CalcNonConservativePower().

#include <drake/multibody/tree/linear_bushing_roll_pitch_yaw.h>

Public Member Functions
	LinearBushingRollPitchYaw (const Frame< T > &frameA, const Frame< T > &frameC, const Vector3< double > &torque_stiffness_constants, const Vector3< double > &torque_damping_constants, const Vector3< double > &force_stiffness_constants, const Vector3< double > &force_damping_constants)
	Construct a LinearBushingRollPitchYaw B that connects frames A and C, where frame A is welded to a link L0 and frame C is welded to a link L1. More...
	~LinearBushingRollPitchYaw () override
const RigidBody< T > &	link0 () const
	Returns link (body) L0 (frame A is welded to link L0). More...
const RigidBody< T > &	link1 () const
	Returns link (body) L1 (frame C is welded to link L1). More...
const Frame< T > &	frameA () const
	Returns frame A, which is the frame that is welded to link (body) L0 and attached to the bushing. More...
const Frame< T > &	frameC () const
	Returns frame C, which is the frame that is welded to link (body) L1 and attached to the bushing. More...
const Vector3< double > &	torque_stiffness_constants () const
	Returns the default torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad). More...
const Vector3< double > &	torque_damping_constants () const
	Returns the default torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad). More...
const Vector3< double > &	force_stiffness_constants () const
	Returns the default force stiffness constants [kx ky kz] (units of N/m). More...
const Vector3< double > &	force_damping_constants () const
	Returns the default force damping constants [dx dy dz] (units of N*s/m). More...
SpatialForce< T >	CalcBushingSpatialForceOnFrameA (const systems::Context< T > &context) const
	Calculate F_A_A, the bushing's spatial force on frame A expressed in A. More...
SpatialForce< T >	CalcBushingSpatialForceOnFrameC (const systems::Context< T > &context) const
	Calculate F_C_C, the bushing's spatial force on frame C expressed in C. More...
Does not allow copy, move, or assignment
	LinearBushingRollPitchYaw (const LinearBushingRollPitchYaw &)=delete
LinearBushingRollPitchYaw &	operator= (const LinearBushingRollPitchYaw &)=delete
	LinearBushingRollPitchYaw (LinearBushingRollPitchYaw &&)=delete
LinearBushingRollPitchYaw &	operator= (LinearBushingRollPitchYaw &&)=delete
Vector3< T >	GetTorqueStiffnessConstants (const systems::Context< T > &context) const
	Returns the torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad) stored in context. More...
Vector3< T >	GetTorqueDampingConstants (const systems::Context< T > &context) const
	Returns the torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad) stored in context. More...
Vector3< T >	GetForceStiffnessConstants (const systems::Context< T > &context) const
	Returns the force stiffness constants [kx ky kz] (units of N/m) stored in context. More...
Vector3< T >	GetForceDampingConstants (const systems::Context< T > &context) const
	Returns the force damping constants [dx dy dz] (units of N*s/m) stored in context. More...
void	SetTorqueStiffnessConstants (systems::Context< T > *context, const Vector3< T > &torque_stiffness) const
	Sets the torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad) in context. More...
void	SetTorqueDampingConstants (systems::Context< T > *context, const Vector3< T > &torque_damping) const
	Sets the torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad) in context. More...
void	SetForceStiffnessConstants (systems::Context< T > *context, const Vector3< T > &force_stiffness) const
	Sets the force stiffness constants [kx ky kz] (units of N/m) in context. More...
void	SetForceDampingConstants (systems::Context< T > *context, const Vector3< T > &force_damping) const
	Sets the force damping constants [dx dy dz] (units of N*s/m) in context. More...
Public Member Functions inherited from ForceElement< T >
	ForceElement (ModelInstanceIndex model_instance)
	Default constructor for a generic force element. More...
	~ForceElement () override
ForceElementIndex	index () const
	Returns this element's unique index. More...
void	CalcAndAddForceContribution (const systems::Context< T > &context, const internal::PositionKinematicsCache< T > &pc, const internal::VelocityKinematicsCache< T > &vc, MultibodyForces< T > *forces) const
	(Advanced) Computes the force contribution for this force element and adds it to the output arrays of forces. More...
	ForceElement (const ForceElement &)=delete
ForceElement &	operator= (const ForceElement &)=delete
	ForceElement (ForceElement &&)=delete
ForceElement &	operator= (ForceElement &&)=delete
Public Member Functions inherited from MultibodyElement< T >
virtual	~MultibodyElement ()
ModelInstanceIndex	model_instance () const
	Returns the ModelInstanceIndex of the model instance to which this element belongs. More...
template<typename = void>
const MultibodyPlant< T > &	GetParentPlant () const
	Returns the MultibodyPlant that owns this MultibodyElement. More...
void	DeclareParameters (internal::MultibodyTreeSystem< T > *tree_system)
	Declares MultibodyTreeSystem Parameters at MultibodyTreeSystem::Finalize() time. More...
void	SetDefaultParameters (systems::Parameters< T > *parameters) const
	Sets default values of parameters belonging to each MultibodyElement in parameters at a call to MultibodyTreeSystem::SetDefaultParameters(). More...
	MultibodyElement (const MultibodyElement &)=delete
MultibodyElement &	operator= (const MultibodyElement &)=delete
	MultibodyElement (MultibodyElement &&)=delete
MultibodyElement &	operator= (MultibodyElement &&)=delete

Friends
class	BushingTester
template<typename U >
class	LinearBushingRollPitchYaw

Additional Inherited Members
Methods to make a clone templated on different scalar types.
Specific force element subclasses must implement these to support scalar conversion to other types. These methods are only called from MultibodyTree::CloneToScalar(); users must not call these explicitly since there is no external mechanism to ensure the argument tree_clone is in a valid stage of cloning. In contrast, MultibodyTree::CloneToScalar() guarantees that by when ForceElement::CloneToScalar() is called, all Body, Frame and Mobilizer objects in the original tree (templated on T) to which this ForceElement<T> belongs, have a corresponding clone in the cloned tree (argument tree_clone for these methods). Therefore, implementations of ForceElement::DoCloneToScalar() can retrieve clones from tree_clone as needed. Consider the following example for a SpringElement<T> used to model an elastic spring between two bodies: template <typename T> class SpringElement : public ForceElement<T> { public: // Class's constructor. SpringElement( const RigidBody<T>& body1, const RigidBody<T>& body2, double stiffness); // Get the first body to which this spring is connected. const RigidBody<T>& get_body1() const; // Get the second body to which this spring is connected. const RigidBody<T>& get_body2() const; // Get the spring stiffness constant. double get_stiffness() const; protected: // Implementation of the scalar conversion from T to double. std::unique_ptr<ForceElement<double>> DoCloneToScalar( const MultibodyTree<double>& tree_clone) const) { const RigidBody<ToScalar>& body1_clone = tree_clone.get_variant(get_body1()); const RigidBody<ToScalar>& body2_clone = tree_clone.get_variant(get_body2()); return std::make_unique<SpringElement<double>>( body1_clone, body2_clone, get_stiffness()); } MultibodyTree::get_variant() methods are available to retrieve cloned variants from tree_clone, and are overloaded on different element types. For examples on how a MultibodyTree model can be converted to other scalar types, please refer to the documentation for MultibodyTree::CloneToScalar().
Protected Member Functions inherited from MultibodyElement< T >
	MultibodyElement ()
	Default constructor made protected so that sub-classes can still declare their default constructors if they need to. More...
	MultibodyElement (ModelInstanceIndex model_instance)
	Constructor which allows specifying a model instance. More...
	MultibodyElement (ModelInstanceIndex model_instance, int64_t index)
	Both the model instance and element index are specified. More...
template<typename ElementIndexType >
ElementIndexType	index_impl () const
	Returns this element's unique index. More...
int	ordinal_impl () const
	Returns this element's unique ordinal. More...
const internal::MultibodyTree< T > &	get_parent_tree () const
	Returns a constant reference to the parent MultibodyTree that owns this element. More...
const internal::MultibodyTreeSystem< T > &	GetParentTreeSystem () const
	Returns a constant reference to the parent MultibodyTreeSystem that owns the parent MultibodyTree that owns this element. More...
void	SetTopology (const internal::MultibodyTreeTopology &tree)
	Gives MultibodyElement-derived objects the opportunity to retrieve their topology after MultibodyTree::Finalize() is invoked. More...
systems::NumericParameterIndex	DeclareNumericParameter (internal::MultibodyTreeSystem< T > *tree_system, const systems::BasicVector< T > &model_vector)
	To be used by MultibodyElement-derived objects when declaring parameters in their implementation of DoDeclareParameters(). More...
systems::AbstractParameterIndex	DeclareAbstractParameter (internal::MultibodyTreeSystem< T > *tree_system, const AbstractValue &model_value)
	To be used by MultibodyElement-derived objects when declaring parameters in their implementation of DoDeclareParameters(). More...

Constructor & Destructor Documentation

LinearBushingRollPitchYaw() [1/3]

LinearBushingRollPitchYaw ( const LinearBushingRollPitchYaw< T > &  )

delete

LinearBushingRollPitchYaw() [2/3]

LinearBushingRollPitchYaw ( LinearBushingRollPitchYaw< T > &&  )

delete

LinearBushingRollPitchYaw() [3/3]

LinearBushingRollPitchYaw	(	const Frame< T > &	frameA,
		const Frame< T > &	frameC,
		const Vector3< double > &	torque_stiffness_constants,
		const Vector3< double > &	torque_damping_constants,
		const Vector3< double > &	force_stiffness_constants,
		const Vector3< double > &	force_damping_constants
	)

Construct a LinearBushingRollPitchYaw B that connects frames A and C, where frame A is welded to a link L0 and frame C is welded to a link L1.

Parameters

[in]	frameA	frame A of link (body) L0 that connects to bushing B.
[in]	frameC	frame C of link (body) L1 that connects to bushing B.
[in]	torque_stiffness_constants	[k₀ k₁ k₂] multiply the roll-pitch-yaw angles [q₀ q₁ q₂] to produce the spring portion of the "gimbal" torques τ₀, τ₁, τ₂. The SI units of k₀, k₁, k₂ are N*m/rad.
[in]	torque_damping_constants	[d₀ d₁ d₂] multiply the roll-pitch-yaw rates [q̇₀ q̇₁ q̇₂] to produce the damper portion of the "gimbal" torques τ₀, τ₁, τ₂. The SI units of d₀, d₁, d₂ are N*m*s/rad.
[in]	force_stiffness_constants	[kx ky kz] multiply the bushing displacements [x y z] to form 𝐟ᴋ, the spring portion of the force 𝐟 = [fx fy fz]ʙ. The SI units of kx, ky, kz are N/m.
[in]	force_damping_constants	[dx dy dz] multiply the bushing displacement rates [ẋ ẏ ż] to form 𝐟ᴅ, the damper portion of the force 𝐟 = [fx fy fz]ʙ. The SI units of dx, dy, dz are N*s/m.

Note

The LinearBushingRollPitchYaw class documentation describes the stiffness and damping constants.

The net moment on C about Co is affected by both the gimbal torque and the moment of 𝐟 about Co. Similarly, for the net moment on A about Ao.

math::RollPitchYaw describes the roll pitch yaw angles q₀, q₁, q₂. The position from Ao to Co is p_AoCo_B = x 𝐁𝐱 + y 𝐁𝐲 + z 𝐁𝐳 = [x y z]ʙ.

The ModelInstanceIndex assigned to this by the constructor is the one assigned to frame C, i.e., frameC.model_instance().

Precondition

All the stiffness and damping constants must be non-negative.

~LinearBushingRollPitchYaw()

~LinearBushingRollPitchYaw ( )

override

Member Function Documentation

CalcBushingSpatialForceOnFrameA()

SpatialForce<T> CalcBushingSpatialForceOnFrameA

(

const systems::Context< T > &

context

)

const

Calculate F_A_A, the bushing's spatial force on frame A expressed in A.

F_A_A contains two vectors: the moment of all bushing forces on A about Ao (−𝐭 + p_AoAp × −𝐟) and the net bushing force on A (−𝐟 expressed in A).

Parameters

[in]

context

The state of the multibody system.

See also

CalcBushingSpatialForceOnFrameC().

Exceptions

std::exception

if pitch angle is near gimbal-lock. For more info,

See also

RollPitchYaw::DoesCosPitchAngleViolateGimbalLockTolerance().

CalcBushingSpatialForceOnFrameC()

SpatialForce<T> CalcBushingSpatialForceOnFrameC

(

const systems::Context< T > &

context

)

const

Calculate F_C_C, the bushing's spatial force on frame C expressed in C.

F_C_C contains two vectors: the moment of all bushing forces on C about Co (𝐭 + p_CoCp × 𝐟) and the resultant bushing force on C (𝐟 expressed in C).

Parameters

[in]

context

The state of the multibody system.

See also

CalcBushingSpatialForceOnFrameA().

Exceptions

std::exception

if pitch angle is near gimbal-lock. For more info,

See also

RollPitchYaw::DoesCosPitchAngleViolateGimbalLockTolerance().

force_damping_constants()

const Vector3<double>& force_damping_constants

(

)

const

Returns the default force damping constants [dx dy dz] (units of N*s/m).

Refer to How to choose force stiffness and damping constants for more details.

force_stiffness_constants()

const Vector3<double>& force_stiffness_constants

(

)

const

Returns the default force stiffness constants [kx ky kz] (units of N/m).

Refer to How to choose force stiffness and damping constants for more details.

frameA()

const Frame<T>& frameA

(

)

const

Returns frame A, which is the frame that is welded to link (body) L0 and attached to the bushing.

frameC()

const Frame<T>& frameC

(

)

const

Returns frame C, which is the frame that is welded to link (body) L1 and attached to the bushing.

GetForceDampingConstants()

Vector3<T> GetForceDampingConstants

(

const systems::Context< T > &

context

)

const

Returns the force damping constants [dx dy dz] (units of N*s/m) stored in context.

GetForceStiffnessConstants()

Vector3<T> GetForceStiffnessConstants

(

const systems::Context< T > &

context

)

const

Returns the force stiffness constants [kx ky kz] (units of N/m) stored in context.

GetTorqueDampingConstants()

Vector3<T> GetTorqueDampingConstants

(

const systems::Context< T > &

context

)

const

Returns the torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad) stored in context.

GetTorqueStiffnessConstants()

Vector3<T> GetTorqueStiffnessConstants

(

const systems::Context< T > &

context

)

const

Returns the torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad) stored in context.

The following set of methods allow for access and modification of torque/force stiffness/damping parameters stored in a systems::Context. Refer to How to choose force stiffness and damping constants for more details.

link0()

const RigidBody<T>& link0

(

)

const

Returns link (body) L0 (frame A is welded to link L0).

link1()

const RigidBody<T>& link1

(

)

const

Returns link (body) L1 (frame C is welded to link L1).

operator=() [1/2]

LinearBushingRollPitchYaw& operator= ( LinearBushingRollPitchYaw< T > &&  )

delete

operator=() [2/2]

LinearBushingRollPitchYaw& operator= ( const LinearBushingRollPitchYaw< T > &  )

delete

SetForceDampingConstants()

void SetForceDampingConstants	(	systems::Context< T > *	context,
		const Vector3< T > &	force_damping
	)		const

Sets the force damping constants [dx dy dz] (units of N*s/m) in context.

SetForceStiffnessConstants()

void SetForceStiffnessConstants	(	systems::Context< T > *	context,
		const Vector3< T > &	force_stiffness
	)		const

Sets the force stiffness constants [kx ky kz] (units of N/m) in context.

SetTorqueDampingConstants()

void SetTorqueDampingConstants	(	systems::Context< T > *	context,
		const Vector3< T > &	torque_damping
	)		const

Sets the torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad) in context.

SetTorqueStiffnessConstants()

void SetTorqueStiffnessConstants	(	systems::Context< T > *	context,
		const Vector3< T > &	torque_stiffness
	)		const

Sets the torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad) in context.

torque_damping_constants()

const Vector3<double>& torque_damping_constants

(

)

const

Returns the default torque damping constants [d₀ d₁ d₂] (units of N*m*s/rad).

Refer to How to choose torque stiffness and damping constants for more details.

torque_stiffness_constants()

const Vector3<double>& torque_stiffness_constants

(

)

const

Returns the default torque stiffness constants [k₀ k₁ k₂] (units of N*m/rad).

Refer to How to choose torque stiffness and damping constants for more details.

Friends And Related Function Documentation

BushingTester

friend class BushingTester

friend

LinearBushingRollPitchYaw

friend class LinearBushingRollPitchYaw

friend

---

The documentation for this class was generated from the following file:

• drake/multibody/tree/linear_bushing_roll_pitch_yaw.h